Recommendation Systems - Brief overview of Matrix Factorization

By

Build your own Recommender System within 5 minutes!

The goal of recommendation systems is to predict the rating that a user will give an item that they haven't seen yet.  One type of recommendation system is known as collaborative filtering, where we try to infer the preferences of a user by filling in the missing items in a user-item matrix.

The User-Item Matrix:

Suppose we had a user-item matrix like the one below, where each cell represents what a given user (u) has rated an item (i).  

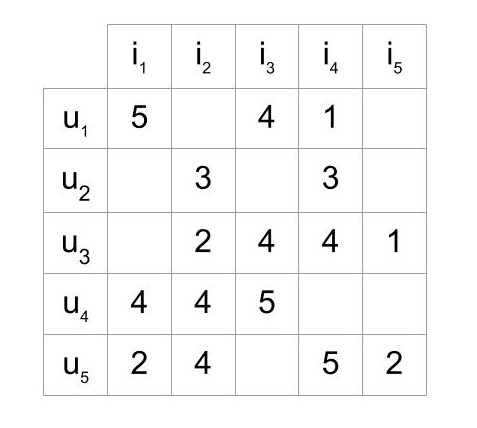
User Item Rating matrix used in recommender systems

There are several missing entries in this matrix, which represent the ratings that we want to predict, and eventually recommend to the user.  If you were working at Netflix, these ratings could mean the number of stars a user has rated a given movie.


Matrix Factorization:

One way of performing collaborative filtering is via matrix factorization.  In matrix factorization, we try to find two low rank matrices U and V, such that when multiplied together, they recreate the original sparse matrix.

Tutorial on Collaborative Filtering and Matrix Factorization


  • The dimensions of the user matrix U is u x d, whether u is the total number of users and d is the number of hidden features.  
  • The dimensions of the item matrix I is d x i, where, again, d is the number of hidden features, and i is the total number of items

These d hidden features represent the hidden attributes for a given user or item, which capture the essence for that given user or item.  For example a given user might have hidden features which represent the degree they like action movies, or the degree they like Disney movies, or their preference for a female or male lead actor.   When a uxd user-factor matrix is multiplied by a dxi item factor matrix, it will create the original uxi user-item matrix with the predicted ratings for the missing values.

Matrix Factorization with Singular Value Decomposition:

We can use a technique such as Singular Value Decomposition (SVD) to decompose the matrix into: 
  • {{U}\in{R^{m \times k}}} , the user factor matrix consisting of m users and k hidden features.
  • {{\Sigma}\in{R^{k \times k}}}  , a diagonal matrix which contains the k singular values of the original matrix
  • {{V}\in{R^{m \times k}}} , the item factor matrix, consisting of n items and k hidden features.
After performing the SVD, the original user-item (mxn) rating matrix A can be reconstructed by multiplying those three matrices together, which would give us our rating predictions:
{{\;A}} = {{U}} \times {{\Sigma }} \times {{{V}}^{{T}}}


One disadvantage of using SVD it that is an analytical approach for decomposing the matrix, requiring that all the values in the matrix to be filled with some value before the SVD can be performed.  

When the matrix becomes too sparse (say less than 1% of the entries of the matrix are filled), then it becomes very difficult to infer these empty items using a traditional SVD.  You can try imputing missing values with the mean of median of a row or column, but this would lead to biased results.  In this case, your SVD would be biased towards computing the mean or median values that you imputed the matrix with.

Matrix Factorization using a Machine Learning Based Approach (ALS):

Alternatively, we can use a machine-learning based approach to learn the user-factor and item-factor matrices. 

Essentially, the goal here is the same as an SVD, we want to learn the two low rank user-factor and item-factor matrices such that when multiplied together, they reconstruct the original sparse user-item matrix.

The Alternating Least Squares algorithm is a popular algorithm for learning the user factor and item factor matrices of a recommendation system.

The objective function we are trying to minimize is the following:



Essentially, we are trying to minimize the difference between , which represents the true ratings, and , which are our predicted ratings, where x is the user-factor matrix of dimensions (num_users, d) and y is the item factor matrix with dimension (d, num_items) .  We also add L2 regularization terms containing the norm of the user factor and item factor matrices, and lambda λ, controlling the strength of the regularization.

Taking the derivative of the cost function with respect to the user-factor matrix x, we can solve for x and get the following:

Similarly, taking the derivative of the cost function with respect to the item-factor y matrix, we can solve for y and get the following:
WNfdfdf
Now that we have these derivatives computed, the ALS algorithm goes as follows:

1. Initialize the user-factor matrix x and item factor y with random numbers.
2. Fixing y, update the user-factor matrix x using the first formula
3. Fixing x, update the item-factor matrix y using the second formula
4. As you keep iterating on steps 2 and 3, the total loss will decrease.  Keep iterating until convergence.

A numpy implementation can be found here:

Additional Resources:
- http://yifanhu.net/PUB/cf.pdf
- http://ethen8181.github.io/machine-learning/recsys/1_ALSWR.html
- https://datasciencemadesimpler.wordpress.com/tag/alternating-least-squares

Comments

Post a Comment

Popular posts from this blog

grandmaster level chess AI using python - Part 2 (the code)

By
Image
In continuation of part 1, I will now building my chess AI in python.  As mentioned before, my goal is to create a chess AI at the Grandmaster level (elo > 2500) Here is the code for the chess AI. https://github.com/luweizhang/chess_ai Key components of the chess game / AI: Python Classes: ChessGame instantiates the chessboard and pieces keeps track of whose turn it is RulesEnforcer Logic for how all the pieces move, castling Makes sure you cant make illegal moves Used in the chess AI to generation possible positions ChessAi Tree generator generates the tree of position moves Position Evaluator evaluates the quality of chess positions Minimax Determines the optimum move from the chess tree ChessDB Opening database Explanation of the tree generator: The tree generator component of the chess AI generates the possible future board positions based on the possible moves that the pieces can make.  At any given position, there are o...
Read more

building a chess ai - part 4: learning an evaluation function using deep learning (keras)

By
Image
Note: this post is still in progress. Below I will discuss approaches for training a deep learning chess game and the results of my implementation. Approach 1: Train against the outcome of the game *y* is the outcome of the game (1 is win for white, 0 is loss for white, .5 is draw) We want to learn a function * f(p)* that can approximate this. *p*  is the chess position (8x8 chess board), actually is an 8x8x12 = 768 dimensional vector (since there are 12 pieces)      8x8x6  = 384 dimensional vector with positive values for squares with a white piece and negative values for squares with a black piece.  (Using 64 x 12 introduces too many degrees of freedom) The goal is to try to learn a function * f(p)* that can predict the winner of the game * y* given a chess position * p* . The model: Dataset: http://www.ficsgames.org/download.html millions of high quality games played by grand masters or international masters Objective/Loss Function...
Read more

Brief intro to recurrent neural networks

By
Image
Note: This post is meant to be a brief and intuitive summary of recurrent neural networks.   I have adapted this material from the Coursera deep learning course.  The value I hope to add here is that I have attempted to summarize the information in a way that is easy (hopefully) to understand, and can be used as reference or refresher material for the future. Part 1: Recurrent Neural Networks: Recurrent neural networks are a class of neural networks where the nodes/neurons form a directed graph along a sequence.  They are very effective at tasks such as Natural Language Processing because they have a "memory," in other words they can receive context from previous inputs.  They can take in input one at a time, and can pass information from one node to the next via hidden activation layers.  This information serves as the "memory" or "context" layer of the network, which can be used in conjunction as more new input is being processed. RNN Cell: ...
Read more