building a chess ai - part 4: learning an evaluation function using deep learning (keras)

Note: this post is still in progress.

Below I will discuss approaches for training a deep learning chess game and the results of my implementation.

Approach 1: Train against the outcome of the game

*y* is the outcome of the game (1 is win for white, 0 is loss for white, .5 is draw)
We want to learn a function *f(p)* that can approximate this.

*p* is the chess position (8x8 chess board), actually is an 8x8x12 = 768 dimensional vector (since there are 12 pieces)   8x8x6  = 384 dimensional vector with positive values for squares with a white piece and negative values for squares with a black piece.  (Using 64 x 12 introduces too many degrees of freedom)

The goal is to try to learn a function *f(p)* that can predict the winner of the game *y* given a chess position *p*.

The model:

• Dataset:
• http://www.ficsgames.org/download.html
• millions of high quality games played by grand masters or international masters
• Objective/Loss Function:
• Train against the outcome of the game
• cross entropy loss function
• argmin y*log(y - f(p)) + (1-y) log(y - f(p))
• y is the actual outcome of the game
• f(p) is the function we are trying to learn 
• Network Architecture
• Maybe a 3 layer deep 2048 wide network???
• Assumptions made and drawbacks
• By trying to predict the outcome of the game given a chess position, we are assuming that the players are playing relatively perfectly here and don't make any mistakes.  In reality, amateur chess players made several blunders throughout the game, even though most of their moves might be optimal or near optimal.  Therefore, in order for the model to perform well, we need a data set consisting of games with perfect or near prefect play.  The best candidates for this type of data is games played by grand masters or games played by other chess computers.

the model architecture is an 8*64 input vector, followed by 3 wide layers with ELU activation followed by a scalar output producted by a softmax layer(probability of winning the game)

Keras code:

(coming soon)

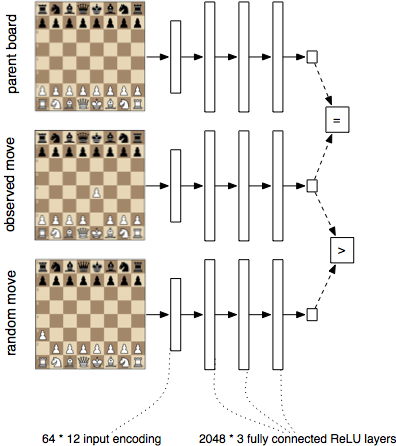
Approach 2:  Try to predict the next move (from Erik Bern blog post)

This is another approach proposed by Erik Bern in his blog post.   Instead of trying to predict the outcome of the game, we try to predict the next move.

The advantage of this method is that now we don't need perfectly played games for training.

Quoting Erik Bern:

Some key assumptions are made here:

1. Players will choose an optimal or near-optimal move. This means that for two position in succession $p\to q$ observed in the game, we will have $f\left(p\right)=-f\left(q\right)$ .
2. For the same reason above, going from $p$ , not to $q$ , but to a randomposition $p\to r$ , we must have $f\left(r\right)>f\left(q\right)$ because the random position is better for the next player and worse for the player that made the move.

How the model is trained:

To train the network, I present it with $(p,q,r)$ triplets. I feed it through the network. Denoting by $S\left(x\right)=1/(1+exp(-x\left)\right)$ , the sigmoid function, the total objective is:

$$su{m}_{(p,q,r)}\log S\left(f\right(q)-f(r\left)\right)+\kappa \log \left(f\right(p)+f(q\left)\right)+\kappa \log (-f(q)-f(p\left)\right)$$

This is the log likelihood of the “soft” inequalities $f\left(r\right)>f\left(q\right)$ , $f\left(p\right)>-f\left(q\right)$ , and $f\left(p\right)<-f\left(q\right)$ . The last two are just a way of expressing a “soft” equality $f\left(p\right)=-f\left(q\right)$ . I also use $\kappa$ to put more emphasis on getting the equality right. I set it to 10.0. I don’t think the solution is super sensitive to the value of $\kappa$ .

Additional Resources:
link to my chess AI repo: https://github.com/luweizhang/chess-ai